一、问题描述

输入一棵二叉搜索树，现在要将该二叉搜索树转换成一个排序的双向链表。而且在转换的过程中，不能创建任何新的结点，只能调整树中的结点指针的指向来实现。

 

二、实现思路

在二叉搜索树中，每个结点都有两个分别指向其左、右子树的指针，左子树结点的值总是小于父结点的值，右子树结点的值总是大于父结点的值。而在双向链表中，每个结点也有两个指针，它们分别指向前一个结点和后一个结点。所以这两种数据结构的结点是一致，二叉搜索树之所以为二叉搜索树，双向链表之所以为双向链表，只是因为两个指针的指向不同而已，通过改变其指针的指向来实现是完全可能的。

 

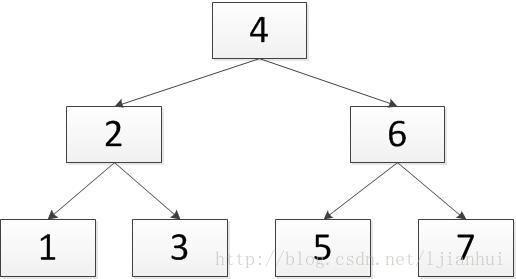
例如如下的二叉搜索树，

 

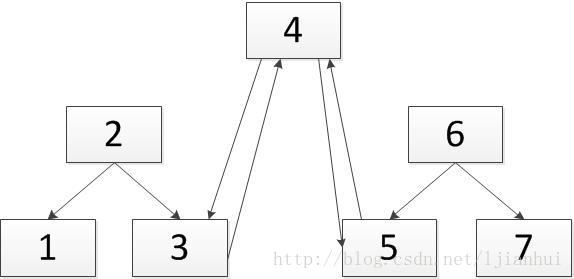
若采用中序遍历，其遍历顺序为1-2-3-4-5-6-7，通过适当的指针变换操作，可变成的双向有序链表如下：

 

 

从上图，我们可以看出，为了减少指针的变换次数，并让操作更加简单，在转换成排序双向链表时，原先指向左子结点的指针调整为链表中指向前一个结点的指针，原先指向右子结点的指针调整为链表中指向下一个结点的指针。例如对于上面的值为2的指点，调整后，它的前一个结点为1，后一个结点为3，而结点2的左子结点本来就为1，右子结点本来就为3.

 

对于树的操作，通常是在遍历树的各个结点的过程中，通过对结点实施某些操作来完成的，这个算法也不例外。由于要求转换后的双向链表也是有序的，而我们从上面也可以看到，当我们以中序遍历二叉搜索树时，其遍历的结点就是有序的，所以在这里我位采用的遍历顺序应该是中序。

 

那么我们应该如何调整指针，让二叉搜索树变成一个双向有序链表呢？当遍历到根结点时，我们可以把树看成三个部分：根结点，根的左子树和根的右子树。如上图的二叉排序树，就分成了根结点4、以结点2为根的左子对和以结点6为根的右子树。从变换的链表中我们可以看到，应当把结点4的left指针指向结点3，把结点3的right指针指向结点4，而由于我们采用的是中序遍历，所以当我们遍历到结点4时，结点4的左子树已经转化为一个有序的双向链表，而结点3是这个已经转化的双向链表的尾结点，所以我们应该用一个变量last_node来保存最后一个结点的指针，以便在与根结点连续时使用。然后把这个变量last_node的值更新为指向根结点4。对于结点4的右子树，采取相似的操作。至于具体的实现，我们只需要对所有的子树递归地执行上述操作即可。其操作过程如下：

 

a]

1. /** 
2. public class TreeNode { 
3.     int val = 0; 
4.     TreeNode left = null; 
5.     TreeNode right = null; 
6.  
7.     public TreeNode(int val) { 
8.         this.val = val; 
9.  
10.     } 
11.  
12. } 
13. */  
14. public class Solution {  
15.     private TreeNode head=null;  
16.     private TreeNode tail=null;  
17.     public TreeNode Convert(TreeNode pRootOfTree) {  
18.         visit(pRootOfTree);  
19.         return head;  
20.     }  
21.     public void visit(TreeNode root) {    
22.         if (root == null) {    
23.             return;    
24.         }    
25.         visit(root.left);    
26.         createList(root);    
27.         visit(root.right);    
28.     }    
29.     public void createList(TreeNode cur){    
30.         cur.left=tail;//把当前的节点接到链表的尾部     
31.         if(tail!=null){//双向连接     
32.             tail.right=cur;     
33.         }else{     
34.             head=cur;     
35.         }     
36.         tail=cur;//更新尾结点为当前结点，或者说：尾结点后移     
37.     }    
38. } 

 

 

 

 

时间复杂度与空间复杂度

该算法首先从根要点一直向左走，找到最左边的结点，其时间复杂度为O(logN)，然后对二叉排序树中的每个结点遍历一次，进行指针变换，其时间复杂度为O(N)，所以总的时间复杂度为O(N)。

 

至于空间复杂度，由于ConvertNode函数进行递归调用，其函数有两个开参，而函数栈中的函数调用层数不会超过树高，所以其空间复杂度为O(logN)。

 

 

分析问题

   

首先需要明白二叉搜索树也是一种排序的数据结构，它的中序遍历就是一个不递减的顺序排列

所以如果要转换成一个排序好的双向链表，那么仅需要改变原来指向左子节点和右子节点的指针，让他们分别指向前节点和后节点即可，如图所示

   

   

调整指针

   

原先指向左子节点的指针调整为链表中指向前一个节点的指针

   

原先指向右子节点的指针调整为链表中指向后一个节点的指针

   

如何调整

   

考虑根节点和左右子树的根本情况，因为如果用递归，这种根本情况考虑就可以去将同样的方法用到左右子树上

   

   

对于这种基本情况，可以分成三个部分来看，根节点10，左子树，右子树，需要做的就是将10与左子树中的最大值连起来，然后把10与右子树中的最小值连起来

   

现在有个问题就是我们并不知道左子树中的最大值和右子树中的最小值，如果我们知道就好了。但是想到递归，递归到左子树中，如果左子树已转换为双向链表，那么双向链表的最后一个节点就是我们想要的，而右子树中的第一个节点也是我们想要的

   

转换代码

   

public static BinaryTreeNode baseconvert(BinaryTreeNode root, BinaryTreeNode lastNode) {

if (root == null)

return lastNode;

BinaryTreeNode current = root;

if (current.leftNode != null)

lastNode=baseconvert(current.leftNode, lastNode);

current.leftNode = lastNode;

if (lastNode != null)

lastNode.rightNode = current;

lastNode = current;

if (current.rightNode != null)

lastNode=baseconvert(current.rightNode, lastNode);

return lastNode;

}

   

要说明的一点是，剑指Offer书上是用C++写的，Java写的时候有点不同，就是baseconvert也要指定返回值，不然会报nullpointer的错误，估计是因为java中只是对象的引用，不然每次返回的lastNode都是空

   

上面的代码中有两个参数，一个是根节点，一个是已经转换好的链表的最后一个节点，因为二叉搜索树中序遍历的特性，当遍历到根节点的时候，左子树已经排好序了，所以会有一个左子树已经转换好的链表，而这个链表的最后一个节点即是我们需要和根节点左连的节点

   

最开始的时候lastNode为null

   

current为当前子树的根节点

   

如果左子树存在，那么转换左子树，递归下去，递归返回之后，说明找到了链表的第一个节点，也就是4那个节点，将4的前面节点置为null，此时current为4那个节点，这个时候由于6的4这个左子树已遍历完了，所以需要往上层返回，返回之前需要将current赋值给lastNode，说明4这个左子树的最后一个节点就是4

   

由于往上返回了一层，此时的current已经是6了，将6的左节点赋值为之前返回的4，判断之前返回的lastNode是否为null，不为空说明需要把根节点和lastNode连起来，其实lastNode为null的情况就只有第一个节点会出现，其他的时候都不会出现。现在已排好序的包括6的左子树以及6本身了，所以此时的lastNode为6

   

6和4的双向连接就完成了，由于6的右子树存在，又会递归到右边子树去，由于8不存在左右子树，递归下去一层之后current就是8这个节点，但它的左孩子为空，所以不会左边递归下去，将8的左连接与之前的lastNode连接起来，建立双向连接的一条连接，然后由于lastNode不为空，所以又把lastNode的右连接与8连接起来，至此双向连接建立，此时lastNode为8

   

所以468都已排好序，此时lastNode为8，返回到上一层，也就是根节点10了，在这一层current为10，将current的左连接与lastNode连接起来，如果lastNode存在，将lastNode的右连接与10连接一起，以此建立双向连接。至此就将根节点和左子树都连接起来了，然后就是去转换右子树，现在的lastNode为10，current为14，14有左孩子，所以需要递归到下一层，下一层的current为12，12没有左孩子，所以不用在坐递归，所以12是12这棵子树转换成双向链表的最左边的节点，将lastNode与12连接，也就是10与12连接，此时的lastNode就变成了12，再将12的右子树递归，由于没有右子树，所以直接返回到上一层，上一层的current是14,14与已排好序的lastNode连接，也就是12与14连接，然后lastNode变为14，递归到14的右子树，也就current变为16，16再递归左子树，无左子树，将16与14连接，此时的lastNode变为16，递归右子树，无右子树，所以整个递归工作完成

   

找到头节点

   

之前的转换只是把引用乾坤大挪移了一下，其实可以发现引用的个数并没有变化，而且头尾节点只有一个出度的引用，而现在我们如果要使用这个双向链表，需要找到头节点

   

public static BinaryTreeNode convert(BinaryTreeNode root) {

BinaryTreeNode lastNode = null;

lastNode=baseconvert(root, lastNode);

BinaryTreeNode headNode = lastNode;

while (headNode.leftNode != null)

headNode = headNode.leftNode;

return headNode;

}

   

测试代码

   

public static void main(String[] args) {

// TODO Auto-generated method stub

BinaryTreeNode root = new BinaryTreeNode(10);

BinaryTreeNode six=new BinaryTreeNode(6);

BinaryTreeNode four=new BinaryTreeNode(4);

BinaryTreeNode eight=new BinaryTreeNode(8);

BinaryTreeNode fourteen=new BinaryTreeNode(14);

BinaryTreeNode twelve=new BinaryTreeNode(12);

BinaryTreeNode sixteen=new BinaryTreeNode(16);

root.leftNode=six;

root.rightNode=fourteen;

six.leftNode=four;

six.rightNode=eight;

four.leftNode=null;

four.rightNode=null;

eight.leftNode=null;

eight.rightNode=null;

fourteen.leftNode=twelve;

fourteen.rightNode=sixteen;

twelve.leftNode=null;

twelve.rightNode=null;

sixteen.rightNode=null;

sixteen.leftNode=null;

BinaryTreeNode result=convert(root);

//                BinaryTreeNode result=baseconvert(root, null);

while (result!=null) {

System.out.println(result.data);

result=result.rightNode;

}